publications
ordered by type and year
Pre-Prints
2025
-
 Explaining Neural Networks with ReasonsLevin Hornischer, and Hannes Leitgeb2025
Explaining Neural Networks with ReasonsLevin Hornischer, and Hannes Leitgeb2025We propose a new interpretability method for neural networks, which is based on a novel mathematico-philosophical theory of reasons. Our method computes a vector for each neuron, called its reasons vector. We then can compute how strongly this reasons vector speaks for various propositions, e.g., the proposition that the input image depicts digit 2 or that the input prompt has a negative sentiment. This yields an interpretation of neurons, and groups thereof, that combines a logical and a Bayesian perspective, and accounts for polysemanticity (i.e., that a single neuron can figure in multiple concepts). We show, both theoretically and empirically, that this method is: (1) grounded in a philosophically established notion of explanation, (2) uniform, i.e., applies to the common neural network architectures and modalities, (3) scalable, since computing reason vectors only involves forward-passes in the neural network, (4) faithful, i.e., intervening on a neuron based on its reason vector leads to expected changes in model output, (5) correct in that the model’s reasons structure matches that of the data source, (6) trainable, i.e., neural networks can be trained to improve their reason strengths, (7) useful, i.e., it delivers on the needs for interpretability by increasing, e.g., robustness and fairness.
@unpublished{Hornischer2025b, author = {Hornischer, Levin and Leitgeb, Hannes}, title = {Explaining Neural Networks with Reasons}, year = {2025}, eprint = {2505.14424}, archiveprefix = {arXiv}, primaryclass = {cs.LG}, url = {https://arxiv.org/abs/2505.14424}, doi = {https://doi.org/10.48550/arXiv.2505.14424}, } -
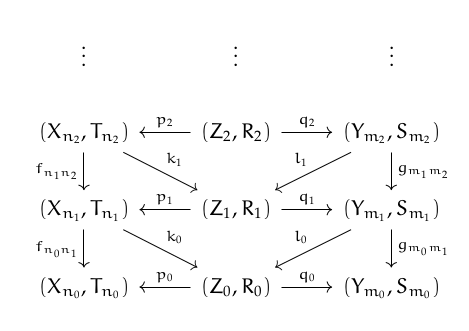 Universal Analog Computation: Fraïssé Limits of Dynamical SystemsLevin Hornischer2025
Universal Analog Computation: Fraïssé Limits of Dynamical SystemsLevin Hornischer2025Analog computation is an alternative to digital computation, that has recently re-gained prominence, since it includes neural networks and neuromorphic computing. Further important examples are cellular automata and differential analyzers. While analog computers offer many advantages, they lack a notion of universality akin to universal digital computers. Since analog computers are best formalized as dynamical systems, we review scattered results on universal dynamical systems. We identify four senses of universality and connect to the two main general theories of computation: coalgebra and domain theory. For nondeterministic systems, we construct a universal system as a Fraïssé limit. It not only is universal in many of the identified senses, it also is unique in additionally being homogeneous. For deterministic systems, a universal system cannot exist, but we provide a simple method for constructing subclasses of deterministic systems with a universal and homogeneous system. This way, we introduce sofic proshifts: those systems that are limits of sofic shifts. In fact, their universal and homogeneous system even is a limit of shifts of finite type and has the shadowing property.
@unpublished{Hornischer2029, author = {Hornischer, Levin}, title = {Universal Analog Computation: Fra\"iss\'e Limits of Dynamical Systems}, year = {2025}, eprint = {2510.10184}, archiveprefix = {arXiv}, primaryclass = {math.DS}, url = {https://arxiv.org/abs/2510.10184}, doi = {https://doi.org/10.48550/arXiv.2510.10184}, }
Journal Articles
2026
-
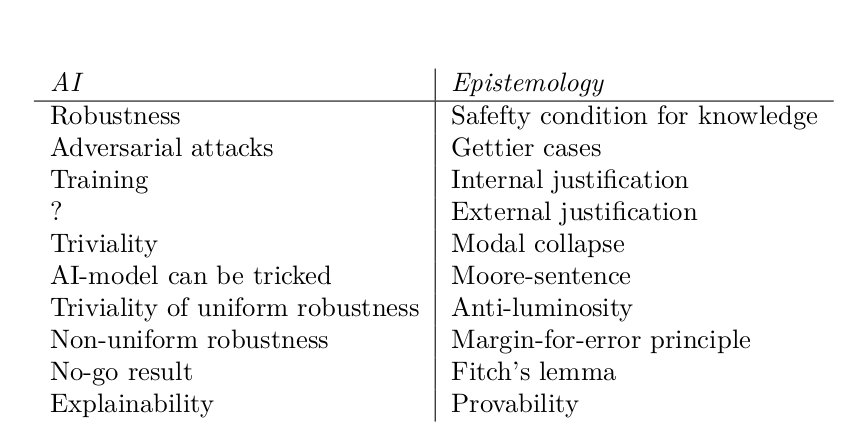 Robustness and Trustworthiness in AI: A No-Go Result From Formal EpistemologyLevin HornischerSynthese, 2026
Robustness and Trustworthiness in AI: A No-Go Result From Formal EpistemologyLevin HornischerSynthese, 2026A major issue for the trustworthiness of modern AI-models is their lack of robustness. A notorious example is that putting a small sticker on a stop sign can cause AI-models to classify it as a speed limit sign. This is not just an engineering challenge, but also a philosophical one: we need to better understand the concepts of robustness and trustworthiness. Here, we contribute to this using methods from (formal) epistemology and prove a no-go result: No matter how these concepts are understood exactly, they cannot have four prima facie desirable properties without trivializing. To do so, we describe a modal logic to reason about the robustness of an AI-model, and then we prove that the four properties imply triviality via a novel interpretation of Fitch’s lemma. We then discuss the consequences for explicating a viable notion of robustness for AI. A broader theme of the paper is to build bridges between AI and epistemology: Not only does epistemology provide novel methods for AI, but modern AI also provides many new questions and perspectives for epistemology.
@article{Hornischer2028, author = {Hornischer, Levin}, journal = {Synthese}, title = {Robustness and Trustworthiness in AI: A No-Go Result From Formal Epistemology}, year = {2026}, number = {22}, pages = {1--37}, volume = {207}, doi = {https://doi.org/10.1007/s11229-025-05272-4}, }
2025
-
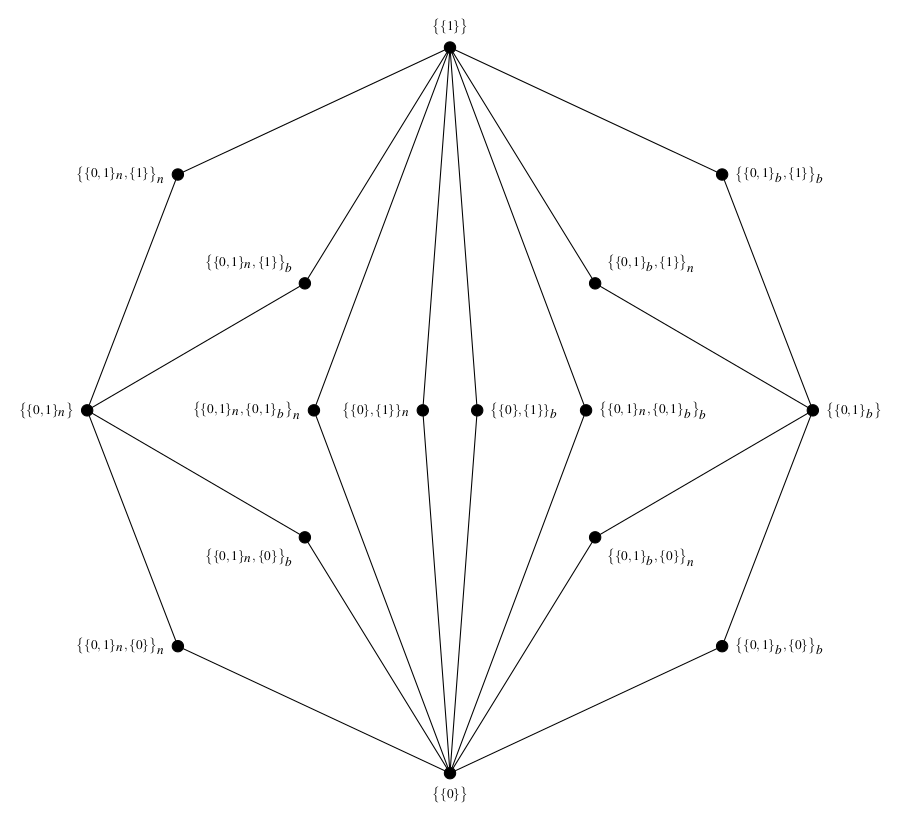 Iterating Both and Neither: With Applications to the ParadoxesLevin HornischerNotre Dame Journal of Formal Logic, 2025
Iterating Both and Neither: With Applications to the ParadoxesLevin HornischerNotre Dame Journal of Formal Logic, 2025A common response to the paradoxes of vagueness and truth is to introduce the truth-values ’neither true nor false’ or ’both true and false’ (or both). However, this infamously runs into trouble with higher-order vagueness or the revenge paradox. This, and other considerations, suggest iterating ’both’ and ’neither’: as in ’neither true nor neither true nor false’. We present a novel explication of iterating ’both’ and ’neither’. Unlike previous approaches, each iteration will change the logic, and the logic in the limit of iteration is an extension of paraconsistent quantum logic. Surprisingly, we obtain the same limit logic if we use (a) both and neither, (b) only neither, or (c) only neither applied to comparable truth-values. These results promise new and fruitful replies to the paradoxes of vagueness and truth. (The paper allows for modular reading: for example, half of it is an appendix studying involutive lattices to prove the results.)
@article{Hornischer2025, author = {Hornischer, Levin}, journal = {Notre Dame Journal of Formal Logic}, title = {Iterating Both and Neither: With Applications to the Paradoxes}, year = {2025}, doi = {10.1215/00294527-2024-0038}, } -
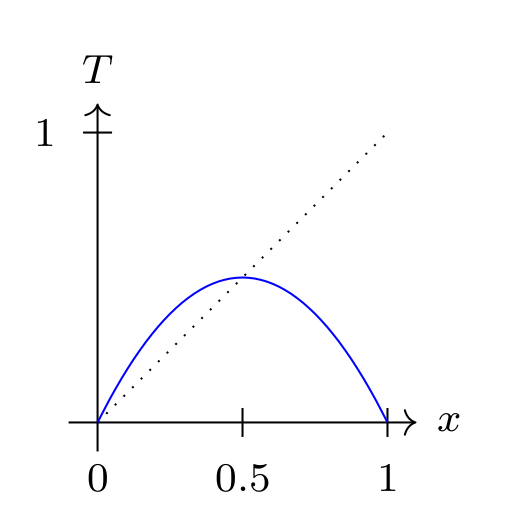 The Logic of Dynamical Systems is RelevantLevin Hornischer, and Francesco BertoMind, 2025
The Logic of Dynamical Systems is RelevantLevin Hornischer, and Francesco BertoMind, 2025Lots of things are usefully modelled in science as dynamical systems: growing populations, flocking birds, engineering apparatus, cognitive agents, distant galaxies, Turing machines, neural networks. We argue that relevant logic is ideal for reasoning about dynamical systems, including interactions with the system through perturbations. Thus, dynamical systems provide a new applied interpretation of the abstract Routley-Meyer semantics for relevant logic: the worlds in the model are the states of the system, while the (in)famous ternary relation is a combination of perturbation and evolution in the system. Conversely, the logic of the relevant conditional provides sound and complete laws of dynamical systems.
@article{Hornischer2026, author = {Hornischer, Levin and Berto, Francesco}, journal = {Mind}, title = {The Logic of Dynamical Systems is Relevant}, year = {2025}, doi = {https://doi.org/10.1093/mind/fzaf012}, } -
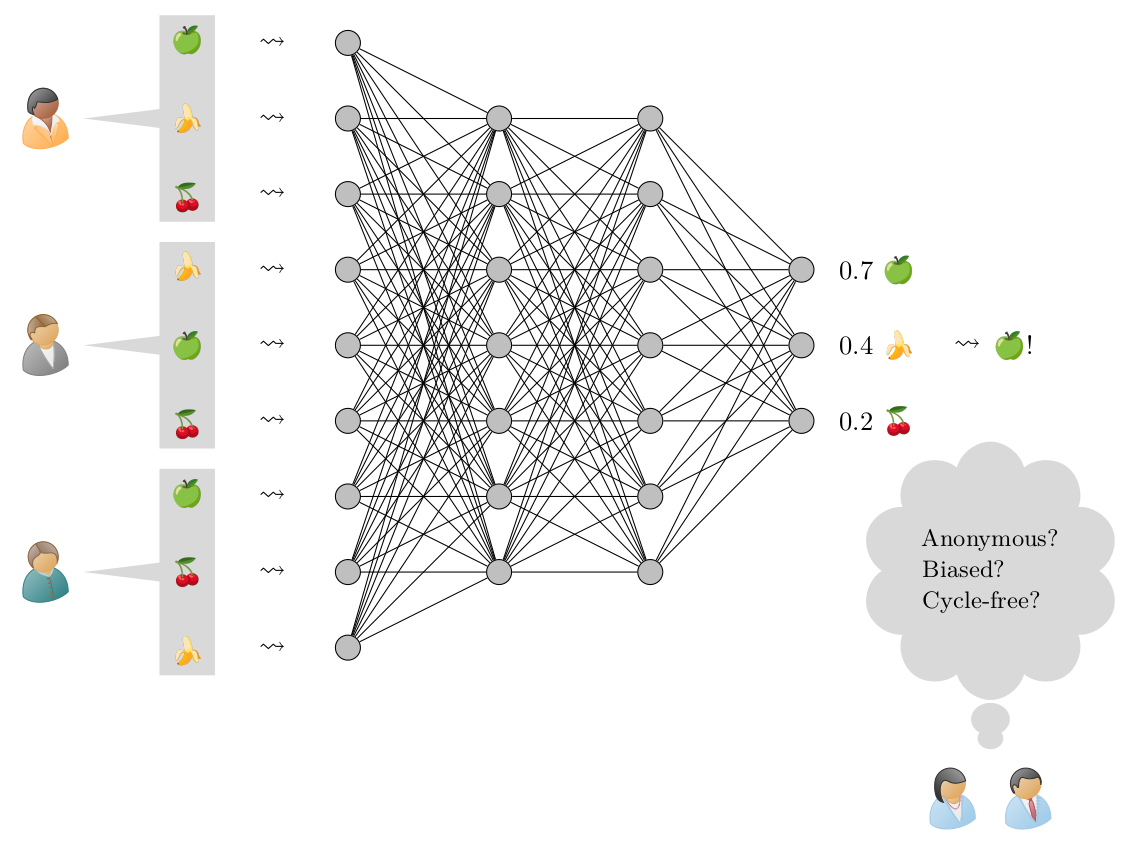 Learning How to Vote With Principles: Axiomatic Insights Into the Collective Decisions of Neural NetworksLevin Hornischer, and Zoi TerzopoulouJournal of Artificial Intelligence Research, 2025
Learning How to Vote With Principles: Axiomatic Insights Into the Collective Decisions of Neural NetworksLevin Hornischer, and Zoi TerzopoulouJournal of Artificial Intelligence Research, 2025Can neural networks be applied in voting theory, while satisfying the need for transparency in collective decisions? We propose axiomatic deep voting: a framework to build and evaluate neural networks that aggregate preferences, using the well-established axiomatic method of voting theory. Our findings are: (1) Neural networks, despite being highly accurate, often fail to align with the core axioms of voting rules, revealing a disconnect between mimicking outcomes and reasoning. (2) Training with axiom-specific data does not enhance alignment with those axioms. (3) By solely optimizing axiom satisfaction, neural networks can synthesize new voting rules that often surpass and substantially differ from existing ones. This offers insights for both fields: For AI, important concepts like bias and value-alignment are studied in a mathematically rigorous way; for voting theory, new areas of the space of voting rules are explored.
@article{Hornischer2027, author = {Hornischer, Levin and Terzopoulou, Zoi}, journal = {Journal of Artificial Intelligence Research}, title = {Learning How to Vote With Principles: Axiomatic Insights Into the Collective Decisions of Neural Networks}, year = {2025}, doi = {https://doi.org/10.1613/jair.1.18890}, }
2024
-
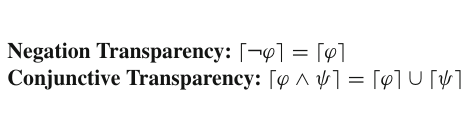 Truth, Topicality, and Transparency: One-Component Versus Two-Component SemanticsPeter Hawke, Levin Hornischer, and Franz BertoLinguistics and Philosophy, 2024
Truth, Topicality, and Transparency: One-Component Versus Two-Component SemanticsPeter Hawke, Levin Hornischer, and Franz BertoLinguistics and Philosophy, 2024When do two sentences say the same thing, that is, express the same content? We defend two-component (2C) semantics: the view that propositional contents comprise (at least) two irreducibly distinct constituents, (1) truth-conditions, and (2) subject-matter. We contrast 2C with one-component (1C) semantics, focusing on the view that subject-matter is reducible to truth- conditions. We identify exponents of this view and argue in favor of 2C. An appendix proposes a general formal template for propositional 2C semantics.
@article{Hawke2024, author = {Hawke, Peter and Hornischer, Levin and Berto, Franz}, journal = {Linguistics and Philosophy}, title = {Truth, Topicality, and Transparency: One-Component Versus Two-Component Semantics}, year = {2024}, doi = {https://doi.org/10.1007/s10988-023-09408-y}, }
2023
-
 Cognitive synonymy: a dead parrot?Francesco Berto, and Levin HornischerPhilosophical Studies, 2023
Cognitive synonymy: a dead parrot?Francesco Berto, and Levin HornischerPhilosophical Studies, 2023Sentences φ and ψ are cognitive synonyms for one when they play the same role in one’s cognitive life. The notion is pervasive (Sect. 1), but elusive: it is bound to be hyperintensional (Sect. 2), but excessive fine-graining would trivialize it and there are reasons for some coarse-graining (Sect. 2.1). Conceptual limitations stand in the way of a natural algebra (Sect. 2.2), and it should be sensitive to subject matters (Sect. 2.3). A cognitively adequate individuation of content may be intransitive (Sect. 3) due to ‘dead parrot’ series: sequences of sentences φ1 , ... , φn where adjacent φi and φi+1 are cognitive synonyms while φ1 and φn are not (Sect. 3.1). Finding an intransitive account is hard: Fregean equipollence won’t do (Sect. 3.2) and a result by Leitgeb shows that it wouldn’t satisfy a minimal compositionality principle (Sect. 3.3). Sed contra, there are reasons for transitivity, too (Sect. 3.4). In Sect. 4, we come up with a formal semantics capturing this jumble of desiderata, thereby showing that the notion is coherent. In Sect. 5, we re-assess the desiderata in its light.
@article{Berto2023, author = {Berto, Francesco and Hornischer, Levin}, journal = {Philosophical Studies}, title = {Cognitive synonymy: a dead parrot?}, year = {2023}, pages = {2727-2752}, volume = {180}, doi = {https://doi.org/10.1007/s11098-023-02007-4}, }
2021
-
 The Logic of Information in State SpacesLevin HornischerThe Review of Symbolic Logic, 2021
The Logic of Information in State SpacesLevin HornischerThe Review of Symbolic Logic, 2021State spaces are, in the most general sense, sets of entities that contain information. Examples include states of dynamical systems, processes of observations, or possible worlds. We use domain theory to describe the structure of positive and negative information in state spaces. We present examples ranging from the space of trajectories of a dynamical system, over Dunn’s aboutness interpretation of fde, to the space of open sets of a spectral space. We show that these information structures induce so-called hype models which were recently developed by Leitgeb (2019). Conversely, we prove a representation theorem: roughly, hype models can be represented as induced by an information structure. Thus, the well-behaved logic hype is a sound and complete logic for reasoning about information in state spaces.
As application of this framework, we investigate information fusion. We motivate two kinds of fusion. We define a groundedness and a separation property that allow a hype model to be closed under the two kinds of fusion. This involves a Dedekind–MacNeille completion and a fiber-space like construction. The proof-techniques come from pointless topology and universal algebra.
@article{Hornischer2021, author = {Hornischer, Levin}, journal = {The Review of Symbolic Logic}, title = {The Logic of Information in State Spaces}, year = {2021}, number = {1}, pages = {155--186}, volume = {14}, doi = {https://doi.org/10.1017/S1755020320000222}, }
2020
-
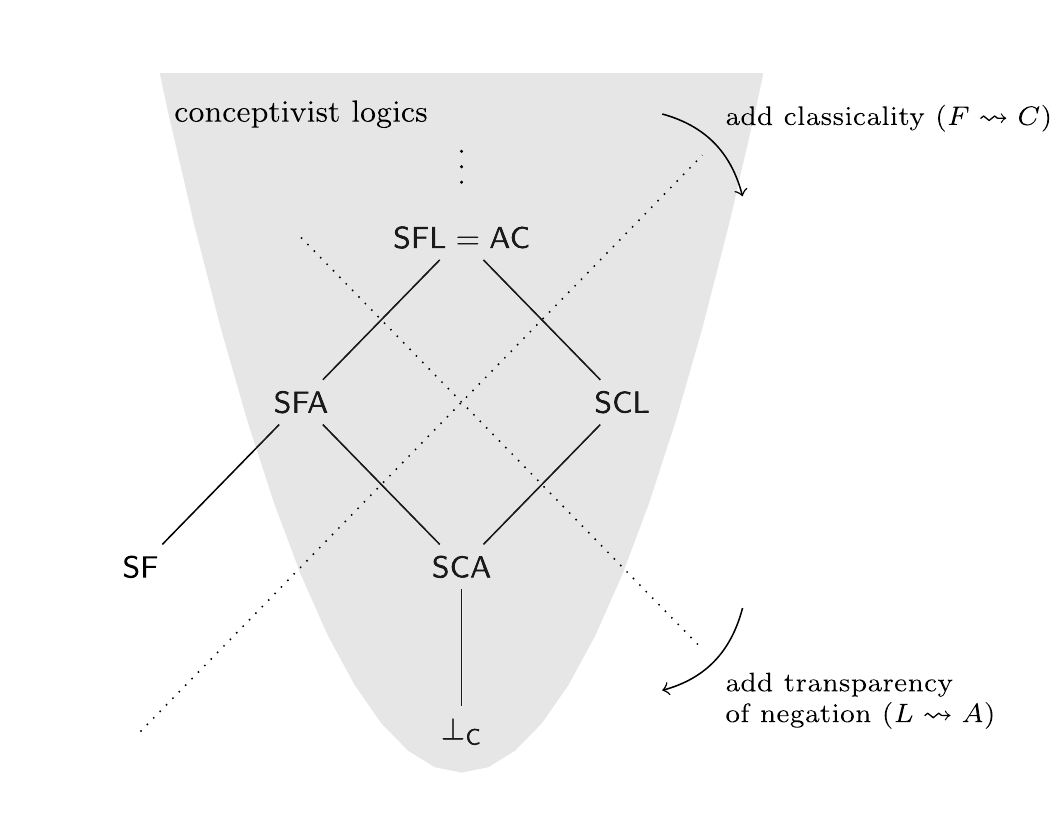 Logics of SynonymyLevin HornischerJournal of Philosophical Logic, 2020
Logics of SynonymyLevin HornischerJournal of Philosophical Logic, 2020We investigate synonymy in the strong sense of content identity (and not just meaning similarity). This notion is central in the philosophy of language and in applications of logic. We motivate, uniformly axiomatize, and characterize several “benchmark” notions of synonymy in the messy class of all possible notions of synonymy. This class is divided by two intuitive principles that are governed by a no-go result. We use the notion of a scenario to get a logic of synonymy (SF) which is the canonical representative of one division. In the other division, the so-called conceptivist logics, we find, e.g., the well-known system of analytic containment (AC). We axiomatize four logics of synonymy extending AC, relate them semantically and proof-theoretically to SF, and characterize them in terms of weak/strong subject matter preservation and weak/strong logical equivalence. This yields ways out of the no-go result and novel arguments—independent of a particular semantic framework—for each notion of synonymy discussed (using, e.g., Hurford disjunctions or homotopy theory). This points to pluralism about meaning and a certain non-compositionality of truth in logic programs and neural networks. And it unveils an impossibility for synonymy: if it is to preserve subject matter, then either conjunction and disjunction lose an essential property or a very weak absorption law is violated.
@article{Hornischer2020, author = {Hornischer, Levin}, journal = {Journal of Philosophical Logic}, title = {Logics of Synonymy}, year = {2020}, pages = {767-805}, volume = {49}, doi = {https://doi.org/10.1007/s10992-019-09537-5}, }
Conference Articles
2019
-
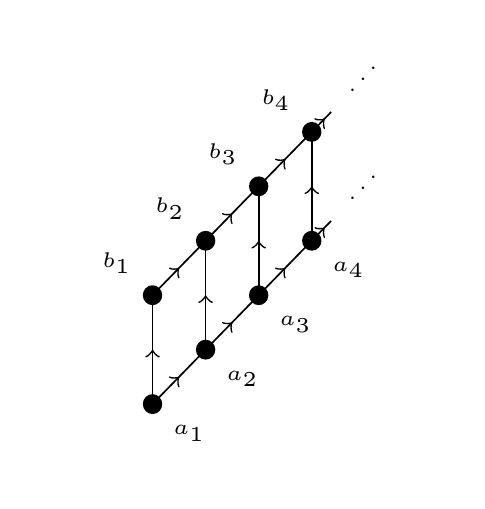 Toward a Logic for Neural NetworksLevin Hornischer2019
Toward a Logic for Neural NetworksLevin Hornischer2019Neural networks and related computing systems suffer from the notorious black box problem: despite their success, we lack a general framework or language to reason about the behavior of these systems. We need a logic with a mathematical semantics for this. In this paper, we sketch a first such logic: a mathematical structure with a logic that describes the behavior of possibly non-deterministic, discrete dynamical systems (which include neural networks).
The mathematical structure is based on domain theory. Domains solved the ‘black box problem’ of (classical) computers by providing a denotational semantics for computer programs. Can it analogously be used for neural networks? We show that, under precise conditions, the possible behaviors of a system form a domain—relating domain theoretic concepts to properties of the system.
This mathematical structure can interpret the well-behaved logic HYPE which thus can be used to reason about both the long-term behavior and the history of the system.
@inproceedings{Hornischer2019, author = {Hornischer, Levin}, booktitle = {The Logica Yearbook 2018}, title = {Toward a Logic for Neural Networks}, year = {2019}, address = {London}, editor = {Sedl{\'a}r, Igor and Blicha, Martin}, pages = {133-148}, publisher = {College Publications}, type = {paper} }
Theses
2021
-
 Dynamical Systems via Domains: Toward a Unified Foundation of Symbolic and Non-symbolic ComputationLevin Hornischer2021PhD Thesis, University of Amsterdam, Institute for Logic, Language and Computation
Dynamical Systems via Domains: Toward a Unified Foundation of Symbolic and Non-symbolic ComputationLevin Hornischer2021PhD Thesis, University of Amsterdam, Institute for Logic, Language and ComputationNon-symbolic computation (as, e.g., in biological and artificial neural networks) is astonishingly good at learning and processing noisy real-world data. However, it lacks the kind of understanding we have of symbolic computation (as, e.g., specified by programming languages). Just like symbolic computation, also non-symbolic computation needs a semantics—or behavior description—to achieve structural understanding. Domain theory has provided this for symbolic computation, and this thesis is about extending it to non-symbolic computation.
Symbolic and non-symbolic computation can be described in a unified framework as state-discrete and state-continuous dynamical systems, respectively. So we need a semantics for dynamical systems: assigning to a dynamical system a ‘domain’ which describes the system’s behavior. A domain is a set of elements ordered by information containment. In our case, the elements are observable behaviors of the system, and one behavior x is informationally contained in another y if what can be learned about the system from x can also be learned from y. Finitely observable behaviors then are ‘compact’ or ‘directly accessible’ elements that can approximate the infinite limit behaviors of the system.
In part 1 of the thesis, we provide this domain-theoretic semantics for the ‘symbolic’ state-discrete systems (i.e., labeled transition systems). And in part 2, we do this for the ‘non-symbolic’ state-continuous systems (known from ergodic theory). This is a proper semantics in that the constructions form functors (in the sense of category theory) and, once appropriately formulated, even adjunctions. Stronger yet, we obtain a categorical equivalence in the continuous case: a complete intertranslatability between systems and domains.
In part 3, we explore how this semantics relates the two types of computation. It suggests that non-symbolic computation is the limit of symbolic computation (in the ‘profinite’ sense). Conversely, if the system’s behavior is fairly stable, it may be described as realizing symbolic computation. The concepts of ergodicity and (algorithmic) randomness help to use and achieve this stability. In the last chapter, we then study the general concept of stability: A novel interpretation of Fitch’s paradox reveals that stability cannot jointly have four desirable properties. This has implications for AI-safety: After all, for a neural network to be safe, we expect it to be stable in the sense of computing the same output on sufficiently similar inputs. The theme here is to explore new applications of established philosophical tools (mostly from epistemology) in the non-symbolic computation of modern AI.
@phdthesis{Hornischer2021a, author = {Hornischer, Levin}, note = {PhD Thesis, University of Amsterdam, Institute for Logic, Language and Computation}, title = {Dynamical Systems via Domains: Toward a Unified Foundation of Symbolic and Non-symbolic Computation}, year = {2021}, url = {https://www.illc.uva.nl/Research/Publications/Dissertations/DS-2021-10.text.pdf} }
2017
-
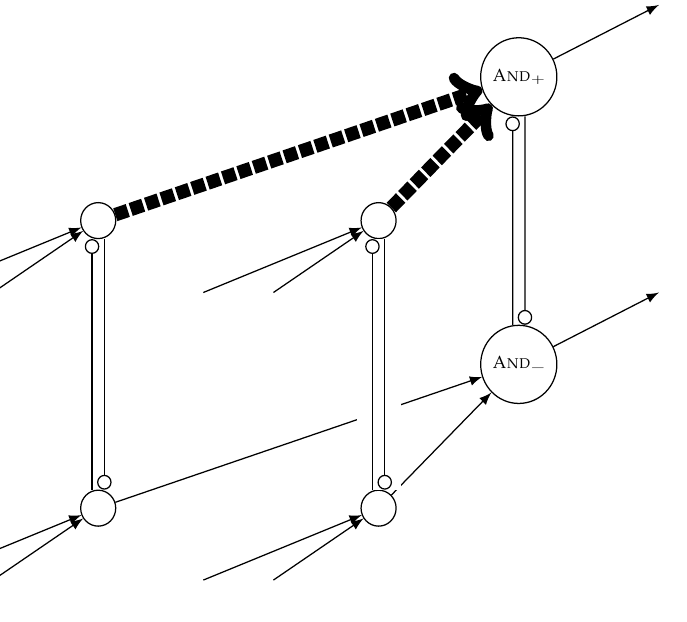 Hyperintensionality and synonymy: a logical, philosophical, and cognitive investigationLevin Hornischer2017Master Thesis, University of Amsterdam, Institute for Logic, Language and Computation
Hyperintensionality and synonymy: a logical, philosophical, and cognitive investigationLevin Hornischer2017Master Thesis, University of Amsterdam, Institute for Logic, Language and Computation@mastersthesis{Hornischer2017, author = {Hornischer, Levin}, note = {Master Thesis, University of Amsterdam, Institute for Logic, Language and Computation}, title = {Hyperintensionality and synonymy: a logical, philosophical, and cognitive investigation}, year = {2017}, url = {https://www.illc.uva.nl/Research/Publications/Reports/MoL-2017-07.text.pdf}, type = {thesis} }